一、教學(xué)目的：

1)  能通過對(duì)不等式應(yīng)用題的理解,，建立數(shù)學(xué)模型,；

2)         掌握利用不等式求最值的方法；

3)         培養(yǎng)學(xué)生主動(dòng)探究,，自覺學(xué)習(xí)的精神,；

激發(fā)學(xué)生創(chuàng)新意識(shí)，開發(fā)學(xué)生的創(chuàng)新潛能,。

二,、教學(xué)重點(diǎn)：建立數(shù)學(xué)模型解決實(shí)際問題

三、教學(xué)難點(diǎn)：利用不等式求函數(shù)最值

四,、教學(xué)方法：啟發(fā)探究式

五,、教學(xué)手段：多媒體電教輔助

六、教學(xué)過程：

（一）  創(chuàng)設(shè)情景,，提出問題：

教師設(shè)計(jì)了一段看似與數(shù)學(xué)無關(guān),，但令學(xué)生十分感興趣的話進(jìn)行引入——

引言： “近十幾年，我們的祖國(guó)在各個(gè)領(lǐng)域取得了矚目的成就,，成為國(guó)際上一個(gè)舉足輕重的國(guó)家，令人驕傲,。特別是近期召開的“十六大”上提出的“全面建設(shè)小康社會(huì)”的國(guó)策更令人鼓舞,。

我們湖大附中繼成為市示范高中之后，又向著省示范高中的目標(biāo)邁進(jìn),！美化校園,、

建設(shè)校園的規(guī)劃工作也進(jìn)入了一個(gè)新的階段,！

李玉新校長(zhǎng)說，希望用最少的錢辦成最好的事,。今天就讓我們一起,，利用大家的智

慧，運(yùn)用數(shù)學(xué)知識(shí)來幫助校長(zhǎng)實(shí)現(xiàn)這個(gè)愿望,�,！�

這番話成功的把學(xué)生的情緒和主人翁意識(shí)調(diào)動(dòng)起來，于是教師“趁熱”將問題拋出

—— 征集“花房工程”的設(shè)計(jì)方案,。

1）利用課件展示“花房工程”：

校園西側(cè)有一面舊墻長(zhǎng)14米,，現(xiàn)準(zhǔn)備利用這面舊墻修建一個(gè)平面圖形為矩形，面積為126米 的花房,。工程條件是：① 修1米舊墻的費(fèi)用為 元,；② 拆去1米舊墻所得的材料修建1米新墻的費(fèi)用為 元；③ 建1米新墻的費(fèi)用為a元,。

2)    請(qǐng)學(xué)生積極思考,，作為設(shè)計(jì)師,設(shè)計(jì)建造花房的不同設(shè)計(jì)方案。啟發(fā)學(xué)生通過

相互討論,，對(duì)各種設(shè)計(jì)方案進(jìn)行理解,、比較。這個(gè)問題設(shè)計(jì)的起點(diǎn)低,，使每個(gè)學(xué)生都可以動(dòng)手,，營(yíng)造一個(gè)“人人參與”的局面，給每個(gè)學(xué)生提供體味成功的機(jī)會(huì),。

(二) 深刻理解,，大膽嘗試：

鼓勵(lì)學(xué)生根據(jù)開放題的敘述，結(jié)合自己的設(shè)計(jì),，口述各種方案施工簡(jiǎn)圖的畫法,。教師通過課件直觀展示繪制簡(jiǎn)圖的過程。通過比較,，認(rèn)識(shí)各種方案的不同之處,。通過歸納，方案大致為兩種：

（方案一）利用舊墻的x米（x<14）,，作為矩形花房的一面邊長(zhǎng),；（方案二）矩形花房的一面邊長(zhǎng)為x米（x 14）.

 

14米

x 米

126米2

（方案一）

 

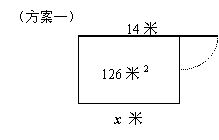
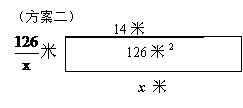
這兩種方案的區(qū)別是：第一種方案有拆舊建新的施工環(huán)節(jié)，而第二種方案則沒有,。

其中的x表示利用舊墻修建的矩形的一邊邊長(zhǎng),，在方案（一）中，0<x<14,；而在方案二中,，x≥14,。同學(xué)們還會(huì)設(shè)計(jì)看似不同于上面兩種的其他方案，但從施工方式的角度來看,，則皆可歸于其中一種,。這個(gè)課件展示過程的目的在于：

（一）直觀校對(duì)學(xué)生繪制簡(jiǎn)圖的正誤；

（二）隱性地啟發(fā)學(xué)生對(duì)簡(jiǎn)圖中每個(gè)量的思考,，為后面問題的進(jìn)一步處理打下基礎(chǔ),。

(三) 探索研究，得出結(jié)論:

將設(shè)計(jì)不同方案的同學(xué)分為幾個(gè)小組,，讓他們計(jì)算自己設(shè)計(jì)的設(shè)計(jì)方案的最低造價(jià),。經(jīng)過同組成員的共同思考、協(xié)作,、互評(píng),，最終選派一名同學(xué)上臺(tái)向大家展示成果。第一種方案將總造價(jià)y表示為關(guān)于x(0<x<14)的函數(shù),利用均值不等式求解: 當(dāng)x=12米時(shí),，最低造價(jià)為35a元,。第二種方案同樣將工程總造價(jià)y表示為關(guān)于x(x≥14)的函數(shù),學(xué)生容易同樣利用均值不等式求解，而實(shí)際上取最值時(shí)等號(hào)成立的條件不成立,。應(yīng)利用函數(shù)的單調(diào)性來解決這個(gè)求最值的問題,，當(dāng)x=14米時(shí)，最低造價(jià)為35.5a元,。對(duì)這個(gè)學(xué)生易錯(cuò)的環(huán)節(jié)絕不能給予事先預(yù)防,，應(yīng)讓學(xué)生充分暴露其思維過程，獲得結(jié)論,。再引導(dǎo)學(xué)生對(duì)自己得到的結(jié)論進(jìn)行全方位的評(píng)析,，自行修改完善，主動(dòng)糾錯(cuò),。這樣,，既可提高學(xué)習(xí)效果，又能優(yōu)化思維品質(zhì),，有助于對(duì)知識(shí)的理解與深化,，自覺形成新舊知識(shí)的結(jié)構(gòu)體系。這就是所謂的“借誤導(dǎo)悟”,。

對(duì)“成果”的評(píng)價(jià)采取自評(píng)和互評(píng)的方式,，選出大家心中的“最佳”方案。讓學(xué)生暢所欲言,，從造價(jià),，施工方式，工期，以及利用土地狀況等諸多因素進(jìn)行考慮,、評(píng)價(jià)。最后,，教師分別從“最實(shí)用性”,、“最少預(yù)算”、“最佳創(chuàng)意”等多個(gè)角度對(duì)每個(gè)設(shè)計(jì)方案進(jìn)行肯定,。充分珍視和保護(hù)每個(gè)學(xué)生的每一個(gè)思維火花,，每一次學(xué)習(xí)激情。

(四) 反思感悟,，小結(jié)要點(diǎn)：

1）   解不等式應(yīng)用問題的步驟：

閱讀理解材料

建立數(shù)學(xué)模型

討論不等關(guān)系

做出問題結(jié)論

2）   利用均值不等式應(yīng)注意的問題：“一正二定三相等”,；

3）   在使用均值不等式求最值時(shí)，若等號(hào)不能取得,，須考慮利用函數(shù)的單調(diào)性求解,。

(五) 學(xué)以致用，開發(fā)潛能：

趁學(xué)生意猶未盡之際,，拿出校園規(guī)劃問題之二 ——

草坪小徑問題

請(qǐng)問怎樣修能使這條小路的長(zhǎng)度最短，用料最�,�,？

將這個(gè)開放性問題留作課堂之外的探究，開放探索空間,，提供更自由的數(shù)學(xué)活動(dòng),。    

最后，送給學(xué)生一段寄語：“今天,，我們?cè)谝黄鹧芯坎⒔鉀Q了一個(gè)身邊看似復(fù)雜,，卻在我們能力范圍之內(nèi)的開放性問題。希望大家今后能夠?qū)W習(xí)用理性的思考,、豐富的知識(shí),，去面對(duì)、去認(rèn)識(shí),、去分析,、去解決學(xué)習(xí)生活中的一切問題！”良好的數(shù)學(xué)品質(zhì)不僅僅只包括數(shù)學(xué)知識(shí),。

七,、課后記：

通過對(duì)這節(jié)開放式授課的設(shè)計(jì)分析，我們不難了解開放式課堂教學(xué)要求教師更新思想，更新教學(xué)態(tài)度,，更新教學(xué)方法,。我們不難看到開放式課堂教學(xué)活動(dòng)，不僅使能力較強(qiáng)的學(xué)生能參加更多的活動(dòng),，同時(shí)也使能力較低的學(xué)生能根據(jù)自己的能力和興趣踴躍參與體驗(yàn)數(shù)學(xué)活動(dòng),。師生之間、學(xué)生之間的多向交流有利于消除傳統(tǒng)授課過于拘謹(jǐn)?shù)膱?chǎng)面,；有利于縮短師生距離,；有利于學(xué)生積極思索，勇于發(fā)現(xiàn),，敢于提出問題,；有利于學(xué)生探究意識(shí)和創(chuàng)新精神的培養(yǎng)和發(fā)揮！給學(xué)生一個(gè)機(jī)會(huì),，他們定會(huì)還你許多驚喜,！